یک ریاضیدان برای سرگرم کردن دوستانش چنین بازی ای را به آن ها پیشنهاد می کند. بازیکنان که تعدادشان دلخواه است کنار هم می نشینند و ریاضیدان ما متوالیا یک تاس را می اندازد و عدد روی آن را اعلام می کند. هر بازیکن باید در طول بازی عددی را به خاطر بسپارد و در مواقع مناسب آن را عوض کند به این شکل که هر بازیکن در مرحله دلخواهی با به خاطر سپردن عدد تاس در آن مرحله که آن را X می گوییم بدون مطلع کردن دیگران وارد بازی می شود. سپس بعد از X مرحله عددی را که در ذهن دارد با عدد روی تاس عوض می کند و به این کار ادامه می دهد.
مثال زیر بازی بازیکنی را نشان می دهد که از مرحله سوم وارد بازی شده است.
| مرحله | ۱ | ۲ | ۳ | ۴ | ۵ | ۶ | ۷ | ۸ | ۹ | ۱۰ | ۱۱ | ۱۲ | ۱۳ | ۱۴ | ۱۵ | ۱۶ | ۱۷ | ۱۸ | ۱۹ |
| عدد تاس | ۵ | ۲ | ۴ | ۳ | ۶ | ۳ | ۱ | ۲ | ۶ | ۳ | ۵ | ۴ | ۲ | ۱ | ۴ | ۲ | ۱ | ۴ | ۶ |
| X | – | – | ۴ | ۴ | ۴ | ۴ | ۱ | ۲ | ۲ | ۳ | ۳ | ۳ | ۲ | ۲ | ۴ | ۴ | ۴ | ۴ | ۶ |
| شمارش مرحلهها | – | – | **** | *** | ** | * | * | ** | * | *** | ** | * | ** | * | **** | *** | ** | * | ****** |
توجه کنید که بجز اعداد روی تاس که از طرف آقای ریاضیدان اعلام می شود هیچ اطلاعات دیگری بین بازیکنان رد و بدل نمی شود و هر بازیکن مراحل بازی را به صورت ذهنی و بدون اطلاع دیگران ادامه می دهد.
بازی مدت زیادی – مثلا ۲۰ تا ۳۰ مرحله – ادامه پیدا می کند. پس از این مدت ریاضیدان ما ناگهان بازی را متوقف می کند و عددی را که بازیکنان در ذهن دارند اعلام می کند. او همچنین ادعا می کند که عدد همه بازیکنان با هم برابر است و همه با کمال شگفتی متوجه می شوند که گفته های او تماما درست است.
یک بار دیگر ماجرا را از نظر بگذرانید: اعداد روی تاس کاملا تصادفی هستند. در ضمن هر بازیکن در مرحله ای دلخواه که دیگران از آن مطلع نیستند وارد بازی شده است. همه چیز به نوعی تردستی یا شعبده بازی شبیه است. به نظر شما ریاضیدان ما چطور می تواند بدون هیچ اطلاعی اعداد بازیکنان را حدس بزند.
سعی کنید راهی برای این کار بیابید. بعد از اینکه به اندازه کافی به این معما فکر کردید میتوانید ادامه مطلب را ببینید.
نمایشی از بازی
بدون توجه به این موضوع که چرا این اتفاق میافتد اگر بپذیریم که عدد موجود در ذهن همه بازیکنان پس از مدتی یکی خواهد شد با کمی دقت خواهیم فهمید کافیست ریاضیدان ما هم مانند بقیه بازی کنان و با همان قواعد بازی کند و بعد از مدتی عدد خود را به بقیه اعلام کند، عددی که برابر با اعداد بقیه خواهد بود.
برای این که بهتر متوجه موضوع شوید، در زیر نمایشی از بازی را میبینید که در آن شما میتوانید به عنوان یک ناظر خارجی روند انتخاب اعداد توسط بازیکن ها را ببینید. ممکن است یکسان شدن اعداد همه ی بازیکنان زمان زیادی طول بکشد، پس کمی صبر داشته باشید. برای آغاز دوبارهی بازی کلید F5 را فشار دهید.
در ضمن لذت آزمایش کردن این بازی را روی دوستان خود از دست ندهید. آنان فوق العاده تعجب خواهند کرد.
چرا اعدادِ همه مساوی میشود؟
![]()

خوب البته موضوع به این سادگیها هم نیست اما تا حدودی میتوان آن را توضیح داد. اگر دقت کرده باشید :
۱ – واضح است که اگر دو نفر همزمان وارد بازی شوند، عدد آنها تا انتهای بازی یکسان باقی خواهد ماند و مثلا اگر نفر اول و سوم در مرحله ۱۰-ام وارد بازی شوند، تا پایان بازی اعدادشان یکسان خواهد ماند. ( به دلیل اینکه آنها در وضعیت یکسانی هستند، پس عددهای آنها هم روند مشابهی را طی خواهد کرد. )
۲ – اگر دو نفر با اعداد مختلف و در مراحل مختلفی وارد بازی شده باشند اعداد آن ها چطور میتوانند با هم مساوی شوند؟
بله، فقط کافی است که این دو نفر در یک مرحله عدد خود را تغییر دهند. برای روشن شدن مطلب بازی دو بازیکن را در بخشی از یک بازی در شکل زیر میبینید:
| تاس | … | ۳ | ۱ | ۴ | ۵ | ۳ | ۶ | ۱ | ۲ | ۶ | ۳ | ۲ | ۴ | ۱ | ۲ | ۲ | ۵ | ۳ | … |
| نفر الف | … | ۲ | ۱ | ۴ | ۴ | ۴ | ۴ | ۱ | ۲ | ۲ | ۳ | ۳ | ۳ | ۱ | ۲ | ۲ | ۵ | ۵ | … |
| نفر ب | … | ۵ | ۵ | ۵ | ۳ | ۳ | ۳ | ۱ | ۲ | ۲ | ۳ | ۳ | ۳ | ۱ | ۲ | ۲ | ۵ | ۵ | … |
در این جدول اعداد سبز نشان دهنده زمانی هستند که یک بازیکن عدد خود را تغییر می دهد. ملاحظه می شود که به محض اینکه دو عدد سبز کنار هم قرار می گیرند، اعدد دو بازیکن یکسان می شود. از آنجا به بعد اعداد یکی باقی می مانند.
حالا به تصویر زیر نگاه کنید. در این تصویر همه مسیرهای ممکن یک بازی را تا مرحله هفدهم میبینید. محور افقی اعداد روی تاس در هر مرحله و محور عمودی اعداد موجود در ذهن بازیکنان را نشان میدهد. از هر ستون یک مسیر خارج میشود که نشان دهنده بازی کسی است که در آن مرحله وارد بازی شده است و یا ادامه بازی کسی را نشان می دهد که در این مرحله عددش را عوض کرده است. با توجه به آنچه قبلا گفتیم اعداد بازیکنانی که انتهای مسیرهایشان در یک ستون باشد یکی می شود، مثلا اعداد بازیکنانی که در مرحله اول یا دوم یا چهارم وارد بازی میشوند در مرحله پنجم یکی میشود و اعداد بازیکنانی که در مرحله ۱۲ و ۱۳ وارد بازی میشوند در مرحله ۱۵ با آنها یکی میشود. و در نهایت عدد همه بازیکنانی که تا قبل از مرحله ۱۷ وارد بازی شدهاند در مرحله ۱۸ یکی میشود.
نکته کلیدی این است که هرچه طول بازی بیشتر میشود احتمال اینکه دو مسیر مجزای بازی در هیچجا با هم و در یک ستون پایان نیابند کمتر و کمتر میشود یعنی به زبان سادهتر وقتی بازی به اندازه کافی ادامه پیدا کند بالاخره جایی پیدا میشود که دو مسیر مجزا در یک ستون و همزمان تمام شوند. اثبات دقیق این موضوع البته مقدماتی نیست اما اگر چند بار به کمک یک تاس جدولی مثل جدول زیر با مقادیر مختلف تاس بسازید میتوانید این نکته را تجربه کنید.
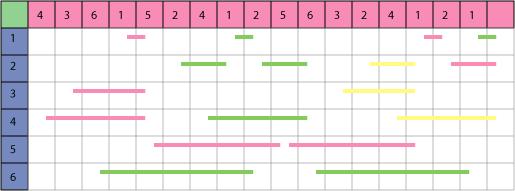
توجه کنید که اگر بازی در مراحل اولیه متوقف شود کاملا ممکن است نتیجه دلخواه بدست نیاید. مثلا در بازی بالا اگر یک بازیکن در مرحله اول و دیگری در مرحله نهم وارد بازی شود و بازی را در مرحله شانزدهم متوقف کنیم عدد بازیکن اول ۱ و عدد بازیکن دوم ۶ خواهد بود. هر چه طول بازی بیشتر باشد احتمال آنکه اعداد همه بازیکنان یکی شود بیشتر است. اینکه چه وقت این احتمال به حد معقولی میرسد البته قابل محاسبه است اما شما با چند بار بازی کردن میتوانید حدود آن را بیابید. پس قبل از اینکه سعی کنید دیگران را با این بازی متعجب کنید حتما کمی آن را تجربه و آزمایش کنید.
بررسی پدیدههایی مثل این بازی منجر به ایجاد شاخهای به نام فرایندهای تصادفی [Stochastic Processes] در ریاضیات شده است که به بررسی رفتار سیستمهای پیچیده و یا تصادفی میپردازد. این شاخه کاربردهای زیادی در بررسی، مدلسازی و تخمینسیستمهای پیچیده طبیعی، فیزیکی، اجتماعی و اقتصادی مثل بازار بورس، گسترش بیماریها و … دارد.
Hits: 0
