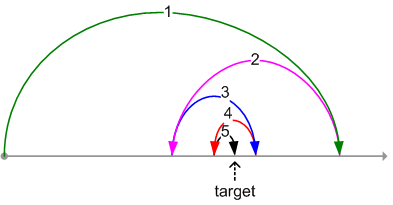
روش نصف کردن اولین و ساده ترین روش برای پیدا کردن صفرهای تابع است ، که البته معایب و محدودیتهایی دارد.این روش برای توابعی قابل اجراست که حول ریشه خود اکیدا یکنوا باشند. به عبارت دیگر این روش تنها برای پیدا کردن ریشه های ساده قابل استفاده است ، و قادر به یافتن ریشه های مضاعف نیست. در ضمن سرعت همگرایی آن بسیار کند است و به همبن دلیل اغلب برای محاسبه صفرهای توابع چند جمله ای (معادلات ساده) استفاده می شود.
الگوریتم روش نصف کردن برای تابعی به نام f به صورت زیر است ، که در آن [a,b] به عنوان بازه حاوی ریشه و عدد e به عنوان میزان دقت به کار رفته است.
۰ – شروع
۱ – اعداد a ، b و e را بگیر.
۲ – (a+b)/2 را در m قرار بده.
۳ – اگر قدرمطلق f(m) کمتر از e بود برو به ۷
۴ – اگر f(a) * f(m) منفی بود m را در b قرار بده
۵ – وگرنه m را در a قرار بده
۶ – برو به ۲
۷ – مقدار m را به عنوان صفر تابع چاپ کن.
۸ – پایان
اکیدا یکنوا بودن تابع حول ریشه اش برای شرط عبارت ۴ الزامی است. این شرط مشخص می کند که ریشه در کدام نصفه بازه قرار دارد.
کد الگوریتم بالا به چهار زبان بیسیک ، سی ، ++C و پاسکال از اینجا قابل دانلود است. برای نتیجه دادن این برنامه ها مقادیر a و b باید به درستی وارد شود. انتخاب بازه ای که شامل ریشه نیست ، حلقه بی نهایت ایجاد می کند. در این برنامه ها از تابع با ضابطه f(x) = x² – ۲ استفاده شده که شما می توانید هر تابع دلخواه دیگری را جایگزین کنید.
Hits: 0
