ستاره داوود ، اختصار نماي ايزومتريك يك مكعب است.
ابتدا بايد بدانيم كه نماي ايزومتريك يك مكعب چيست ؟
اگر يك مكعب را در فضا دوران دهيم ، به گونهاي كه دو راس متقابل به هم در امتداد خط ديد ما قرار بگيرند ، به اين منظره نماي ايزومتريك مكعب گفته ميشود . در واقع نمای ايزومتريك مكعب ، نمايی است كه در آن سه طرف بالا ، راست و چپ مكعب ديده شود ، به انيميشن زير توجه نماييد .
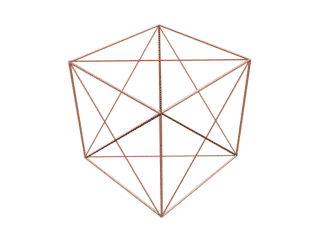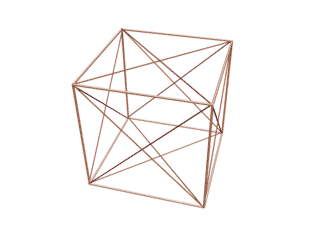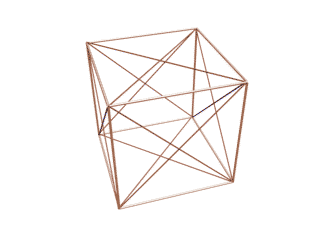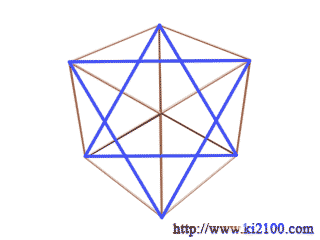
همانطور كه مشخص است انيميشن فوق يك مكعب در حال دوران را نشان ميدهد كه تمامي قطرهاي سطحي ( وجههاي ) آن ، همچنين يالهاي آن رسم شده است كه در نهايت در نماي ايزومتريك متوقف و ستاره داوود كاملا مشخص ميگردد ، البته اين در حالتي خواهد بود كه وجههاي مكعب را از زاويه ديد پنهان نماييم تا خطوط مخفي حجم هويدا شوند ، لازم به توضيح است كه اين ستاره درون يك شش ضلعي منتظم ديده ميشود و چون براي درك بهتر موضوع ، انيميشن فوق در ديد پرسپكتيو تهيه شده است ، شايد اين شش ضلعي ، منتظم بهنظر نرسد . براي واضح بودن رسم ، شكل زير ارايه ميشود .
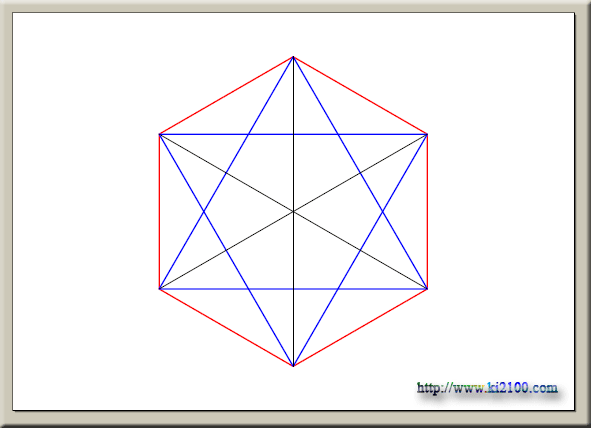
اين رسم هندسي ( ستاره داوود ) به همراه مكعب و شش ضلعي ، نقش بنيادي و كليدي در تمامي عرصههاي علمي ايفا ميكنند . از اين رسم هندسي ستاره داوود با تلفيق و تركيبي از شش ضلعي ، در نقش و نگار مسجد كبود استفاده شده است ، كه دال بر اين موضوع است كه مسلمانان در قديم از اين رسمها در معماريهاي خود استفاده ميكردهاند

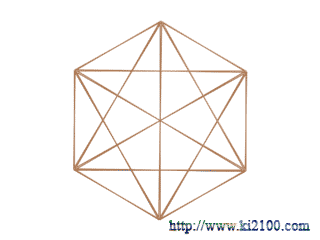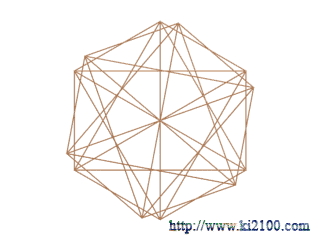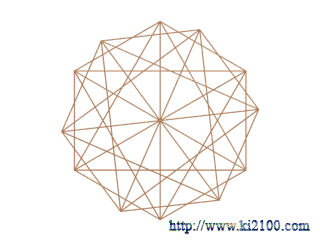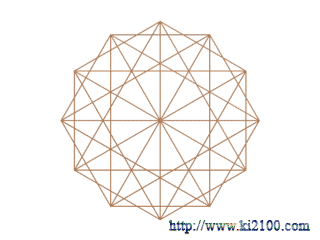
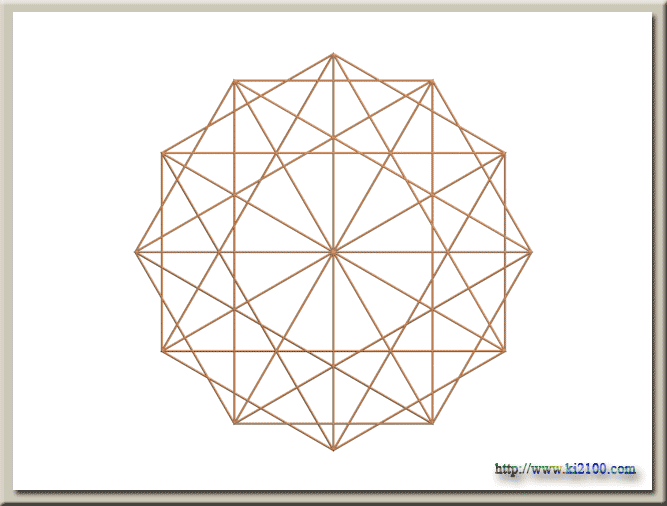
لازم به توضيح است كه اضلاع دوازده ضلعي را رسم نكردهايم ولي راسهاي دوازده ضلعي منتظم مشخص است . براي توسعه رسم فوق در فضاي سه بعدي ، ابتدا آن را حول محور يا قطر عمودي ، در محيط 360 درجه ، شش بار و هر بار 30 درجه دوران ميدهيم ( يعني رسم شماره 4 تصوير زير ) تا كل محيط به دوازده قسمت مساوي تقسيم شود ، سپس اين رسم را به نسبت اندازه خطوط افقي كوچك كرده و پنج بار روي هم ميچينيم ( يعني رسم شماره 1 تصوير زير )
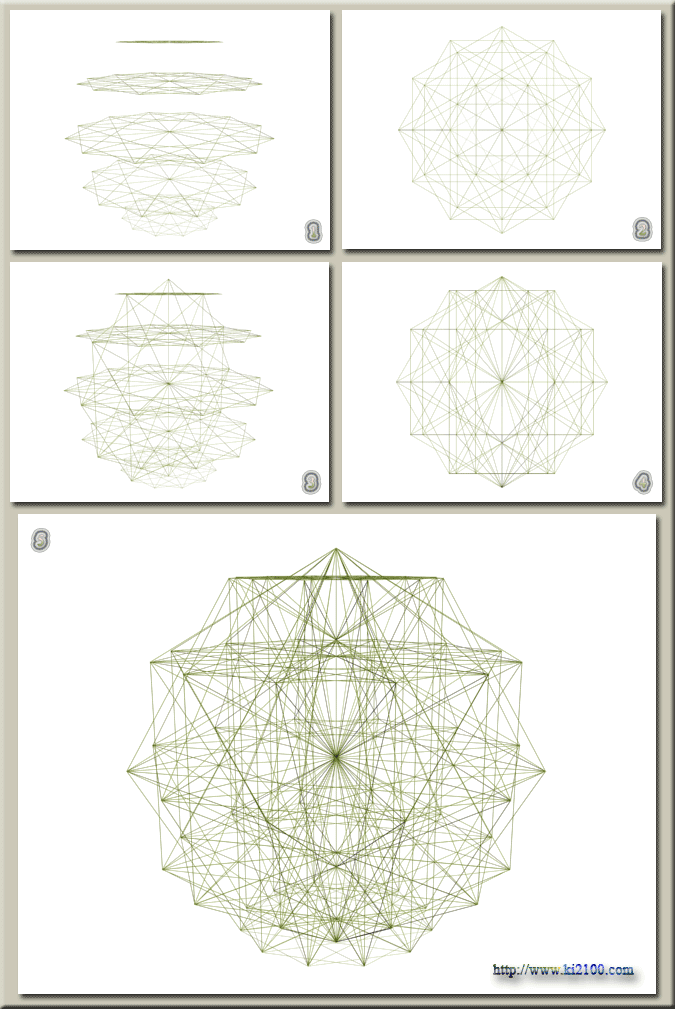
رسم شماره 5 تركيب دو رسم 4 و 1 را نشان ميدهد . رسم شماره 3 كمكي بوده و رسم شماره 2 ، نماي رسم كلي را از بالا نشان ميدهد .
Hits: 13
